A Média Aritmética
A MÉDIA ARITMÉTICA: O que é?
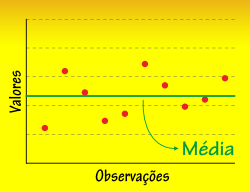Conforme os Parâmetros Curriculares Nacionais, a Média é uma das medidas de tendência central de uma pesquisa, junto com a moda e a mediana.
A Média fornece um indicador que pode representar, em certas circunstâncias, os dados de uma pesquisa e também é a base para o cálculo de outras medidas tais como o desvio padrão, coeficiente de variação, de correlação, dentre outras.
Para que serve a Média Aritmética?
Para estimar uma quantidade desconhecida na presença de erros de medição, que é a diferença entre o valor indicado e o verdadeiro valor medido;
Para obter um valor justo/eqüitativo para uma distribuição uniforme, ou seja, dos valores que tem a mesma chance de ocorrer em um intervalo;
Para servir de elemento representativo de um conjunto de dados, cuja distribuição é simétrica – quando coincidem os valores da média, da moda e da mediana;
Para obter um valor mais provável quando aleatoriamente tomamos um elemento de uma população;
Para ser uma boa estimativa para a média de uma população;
Para ser uma estimativa da variável para tempo futuro.
Imagens: IBGE/CDDI e Freepik
Média Aritmética Simples
A Média Aritmética será chamada de Média Aritmética Simples quando for calculada como o quociente entre a soma de todos os distintos valores relacionados e o número de observações envolvidas nessa soma.
Por exemplo:
Em uma família, de quatro pessoas, a idade do pai é 40, da mãe é 36, do filho é 10 e da filha é 14. Então, qual é a média entre os valores relacionados?
Confira o cálculo no quadro a seguir:
| Pai | Mãe | Filha | Filho | |
|---|---|---|---|---|
| Idades | 40 | 36 | 14 | 10 |
| Soma das idades | 40 + 36 + 14+ 10 = 100 | |||
| Média das idades | 100 ÷ 4 = 25 | |||
Média Aritmética Ponderada
Ela será chamada de Média Aritmética Ponderada quando alguns valores possuírem mais importância (peso) do que outros. Essa relevância é indicada por um numeral denominado peso.
Neste caso, encontraremos a Média Aritmética Ponderada dividindo o somatório dos produtos dos valores por seus respectivos pesos pela soma dos pesos.
Por exemplo:
Em um curso de mecânica, a nota final é obtida após a conclusão de um trabalho prático e duas provas. Mas a organização do curso acha melhor considerar cada prova com diferentes relevâncias. Cada relevância será indicada por um número chamado de peso.
Suponhamos que você esteja fazendo esse curso, então no decorrer do curso você fará um trabalho prático, uma prova com peso 3 e outra prova com peso 6.
No trabalho sua nota foi 8. Na primeira prova sua nota foi 9 e na segunda prova sua nota foi 7.
Então, os valores são: 8 (do trabalho), 9 (da segunda nota que possui peso 3) e 7 (da terceira nota que possui peso 6).
Observação: no caso dos valores que não possuem pesos atribuídos, subentende-se que o peso seja 1.
Confira o cálculo da média ponderada na animação a seguir:
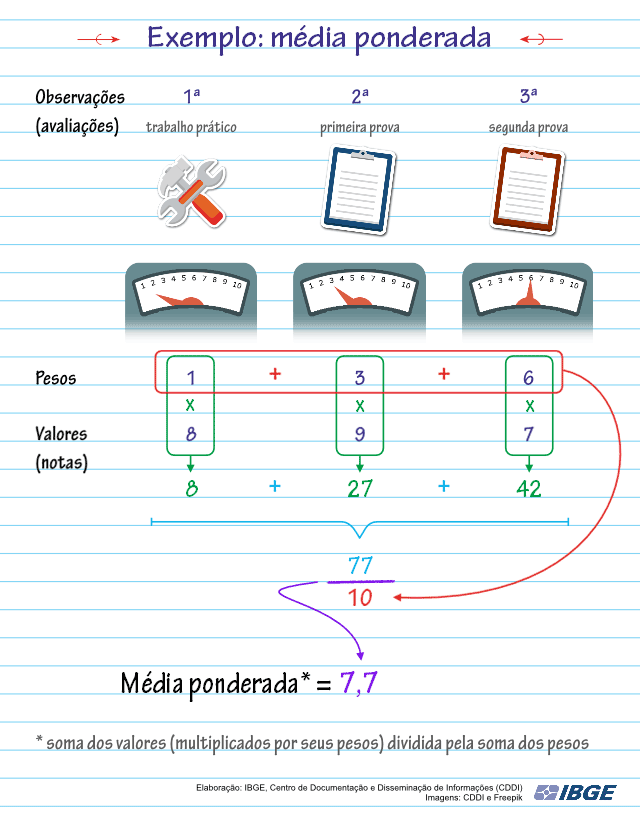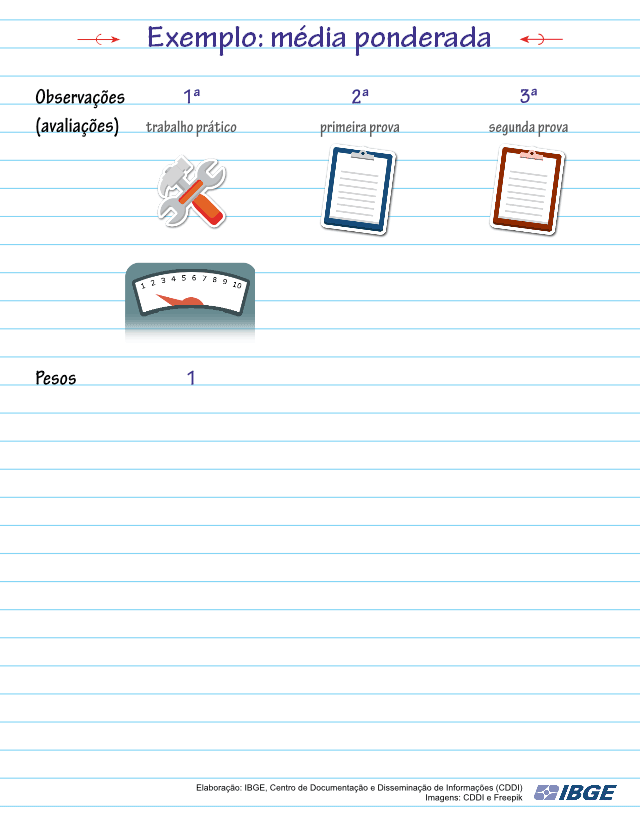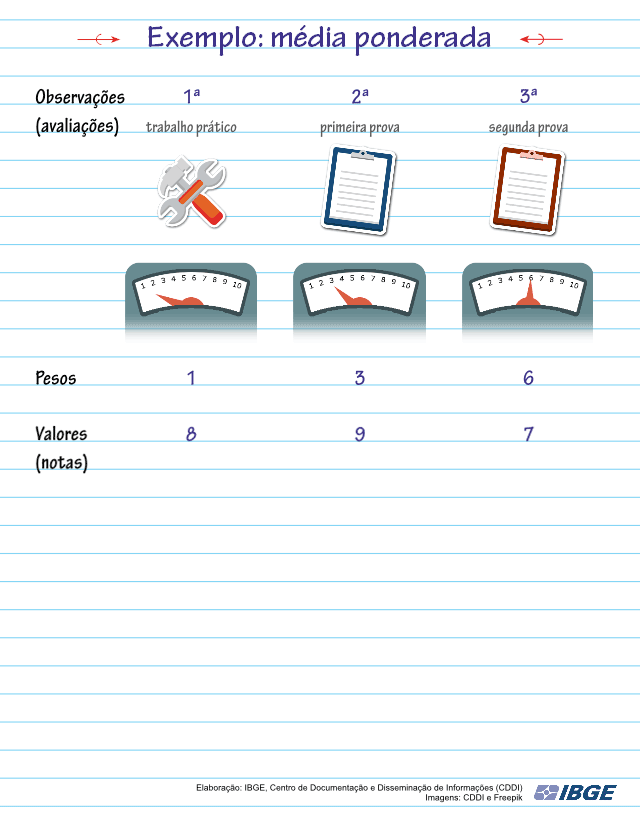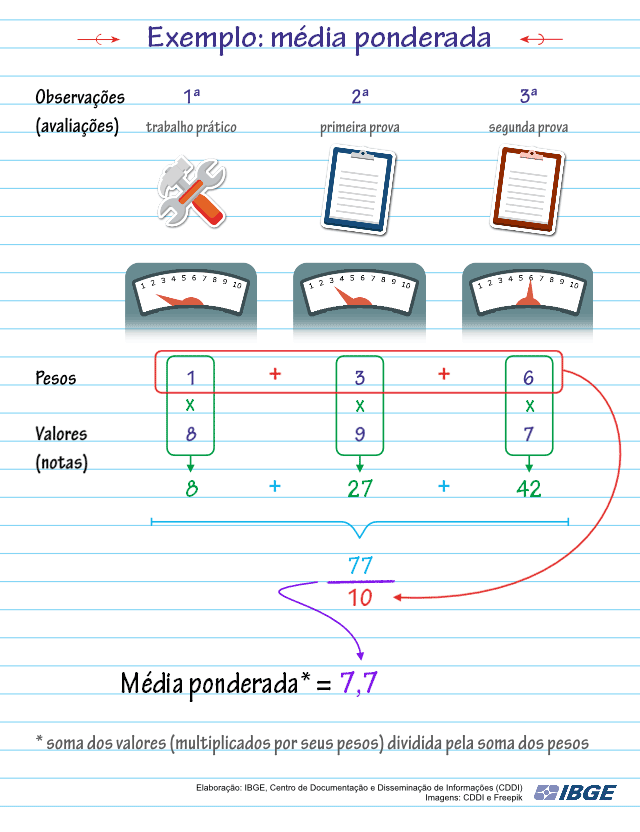
Tanto para a Média Aritmética Simples quanto para a Ponderada:
- A média está localizada entre os valores extremos (valor mínimo e valor máximo)
| Mínimo | < | Média | < | Máximo |
| 10 | < | 25 | < | 40 |
- A soma dos desvios a partir da média é zero
O desvio significa a diferença entre o valor e a média. Mas devemos considerar a posição que a média ocupará no conjunto de valores, após estiverem ordenados:
Assim, os desvios são: (10 - 25), (14 - 25), (36 - 25) e (40 - 25).
Somando os desvios: - 15 - 11 + 11 + 15 = 0.
- A média é influenciada por cada um e por todos os valores;
- A média não necessariamente coincide com um dos valores que a compõem;
- A média pode ser um número que não tem um correspondente na realidade física (por exemplo, em 2000 a mulher brasileira tinha, em média, 2,3 filhos - confira mais dados sobre a fecundidade das brasileiras neste link);
- O cálculo da média leva em consideração todos os valores, inclusive os nulos e os negativos;
- A média é um valor representativo dos dados a partir dos quais ela foi calculada;
- Em termos espaciais, a média é o valor que está mais próximo de todos os valores.
Vejamos um exemplo fictício da Média Aritmética como um boa estimativa para a média de uma população:
Nossa pesquisa será o conjunto formado pelos salários dos 10 empregados de uma empresa.
Qual é a média salarial na empresa? Confira na imagem os valores e o cálculo.
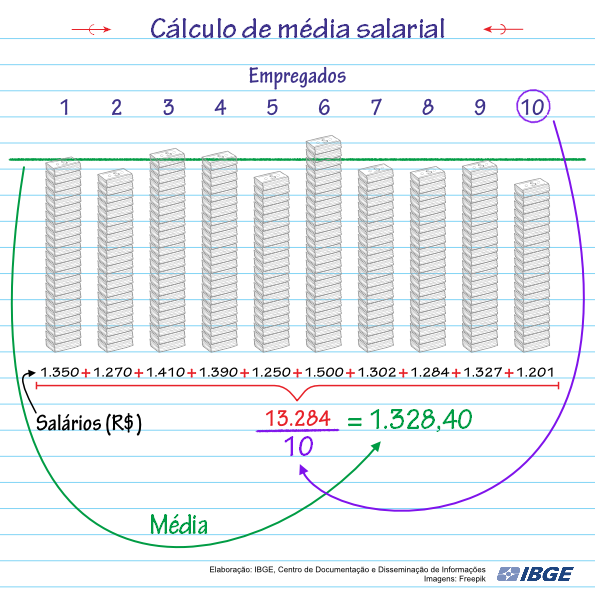
Sendo assim, o valor R$ 1.328,40 representa a média dos dez salários da empresa.
Então o valor R$ 1.328,40 é um elemento que pode representar bem o salário da empresa pesquisada, neste contexto.
Nem sempre a média é a melhor representação de uma realidade. Vejamos alguns exemplos:
Suponhamos que a empresa do exemplo anterior tenha três sócios e, agora, que a esta lista de remunerações também consideremos os valores ganhos pelos sócios mensalmente: R$ 15.000,00 por sócio.
Então, a nova média de salários seria:
Somando todos os salários:
R$ 1350,00 + R$ 1270,00 + R$ 1410,00 + R$ 1390,00 + R$ 1250,00 + R$ 1500,00 + R$ 1302,00 + R$ 1284,00 + R$ 1327,00 + R$ 1201,00 + R$ 15.000,00 + R$ 15.000,00 + R$ 15.000,00 = R$ 58.284,00
Dividindo esta soma pelo total de funcionários mais os sócios (13):
58.284,00 / 13 = 4.483,38
O novo salário médio é de R$ 4.483,38.
Esta nova média, neste contexto, já não é uma boa representação para os salários da empresa pesquisada. A média foi altamente influenciada pelos vencimentos dos três sócios.
Mas, e se a empresa também possuísse 8 estagiários pagando um salário mínimo para cada? Como ficaria a média de salários da empresa, desconsiderando os vencimentos dos sócios?
Somando os vencimentos dos empregados com os dos estagiários, teremos:
R$ 1350,00 + R$ 1270,00 + R$ 1410,00 + R$ 1390,00 + R$ 1250,00 + R$ 1500,00 + R$ 1302,00 + R$ 1284,00 + R$ 1327,00 + R$ 1201,00 + R$ 870,00 + R$ 870,00 + R$ 870,00 + R$ 870,00 + R$ 870,00 + R$ 870,00 + R$ 870,00 + R$ 870,00 = R$ 20.244,00
Então, a nova média será: 20.244,00 / 18 = 1.124,66
O novo salário médio é de R$ 1.124,66.
Também não é, neste contexto, uma boa representação para os salários da empresa pesquisada.
Portanto, percebe-se que os valores correspondentes à média salarial da mesma empresa, nos exemplos mostrados, podem ser: R$ 1.124,66; R$ 1.328,40 e R$ 4.483,38.
Sendo assim, não basta conhecer apenas como calcular a Média Aritmética, é preciso conhecer quais informações fizeram parte desse cálculo para poder obter uma opinião mais próxima da realidade.
Referência Bibliográfica
MAGINA, S.; CAZORLA, I.; GITIRANA, V.; GUIMARÃES, G. Concepções e concepções alternativas de média: um estudo comparativo entre professores e alunos do Ensino Fundamental. Educar em Revista, Curitiba, Brasil, n. especial 2, p. 59-72, 2010. Editora UFPR.