A Mediana

O que é a Mediana?

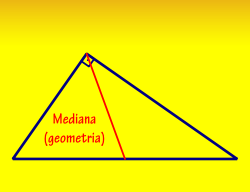Na Geometria é um segmento de reta que liga o vértice de um triângulo qualquer ao ponto médio de seu lado oposto, conforme exemplo do triângulo retângulo na figura ao lado.

Mas, na Estatística, indica o valor médio em um conjunto de números ordenados. Ela indica qual é o valor que está exatamente no meio de um conjunto de dados, quando eles estão ordenados.

A Mediana nos diz que metade (50%) dos valores do conjunto de dados está abaixo dela e a outra metade está acima dela.

Assim como a Média e a Moda, a Mediana é uma medida de tendência central.

No geral, o termo Mediana se refere ao que está entre dois pontos, dois extremos.

Exemplo de cálculo da mediana

Em uma sala de aula foi realizada uma pesquisa onde uma das perguntas era a idade dos alunos. Confira na animação o cálculo da mediana das idades dos alunos:

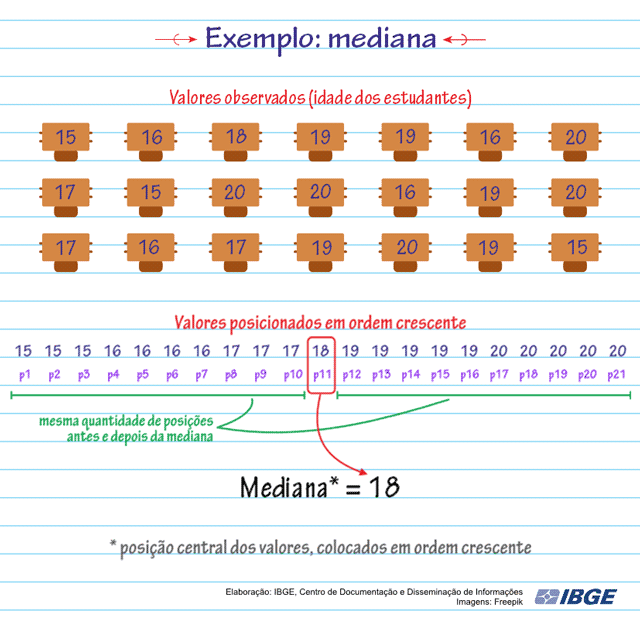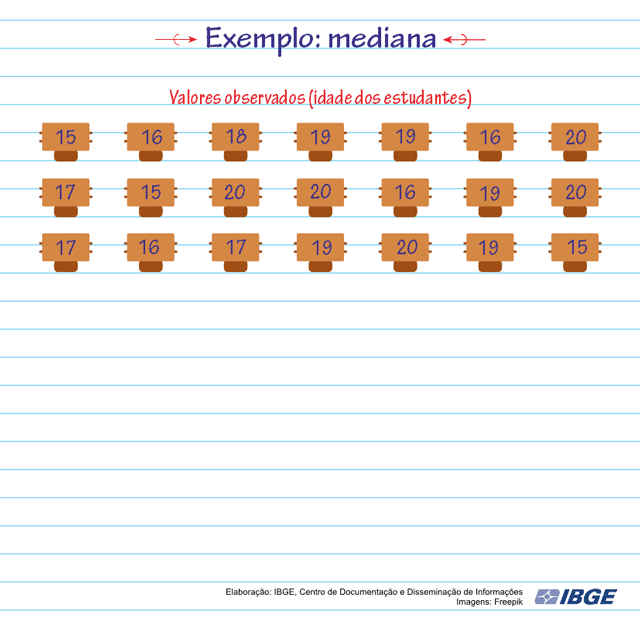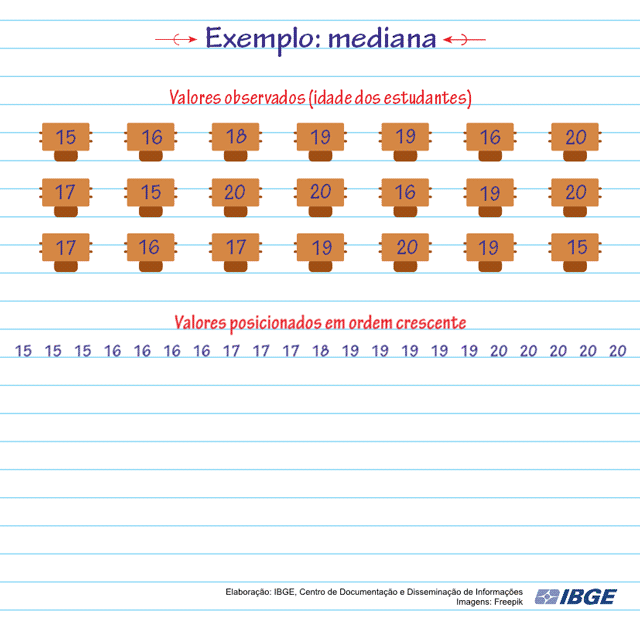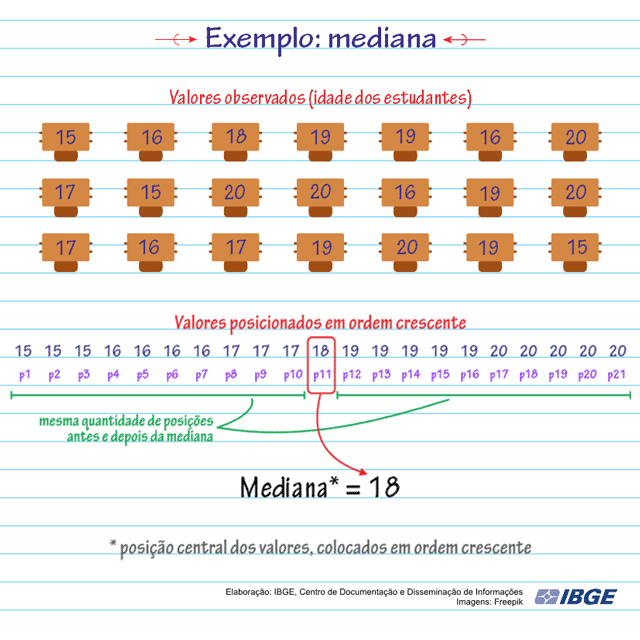
Observe que:
Cada idade ocupa uma posição (de p1 até p21), no conjunto de dados;
As idades estão ordenadas.

A Mediana será a idade: 18, porque ela se encontra exatamente na 11ª posição (p11).

Podemos observar que metade das idades é menor que 18 e a outra metade das idades é maior que 18.

Características da mediana

• Se você tem um conjunto de informações, então a Mediana, que é uma medida de tendência central, indicará exatamente a posição onde será encontrado o valor da amostra que está eqüidistante aos extremos.
• A Mediana nos diz que a quantidade de valores é a mesma tanto antes quanto depois de sua posição.
• A vantagem da Mediana sobre a Média é que a Mediana pode nos fornecer um valor típico do conjunto de dados porque ela não é afetada por valores extremos.
• Podemos considerar a Mediana como uma Média quando o conjunto de dados não é influenciado por valores extremos ou quando há poucos valores extremos, tanto altos quanto baixos.

Como encontramos a Mediana?

Condição primordial para encontrar a Mediana: os elementos da amostra devem estar ordenados de forma crescente ou decrescente.

• Se a quantidade de elementos da amostra (conjunto de dados) for uma quantidade ímpar, então a amostra terá um elemento central e a Mediana será o elemento que se encontra na posição:

( ´Número de elementos da amostra´ + 1 ) dividido por 2

• Se a quantidade de elementos da amostra for uma quantidade par, então a amostra terá dois elementos centrais e a Mediana será a média aritmética entre eles, então:
  Como encontrar a posição dos elementos da amostra para calcular a média entre eles?

Primeiro elemento: ( ´Número de elementos da amostra´ ) dividido por 2;
Segundo elemento: [( ´Número de elementos da amostra´ ) dividido por 2 ] + 1

Exemplo de cálculo da mediana com número ímpar de elementos na amostra

Vamos encontrar a Mediana da população rural do Brasil no Censo de 2010:

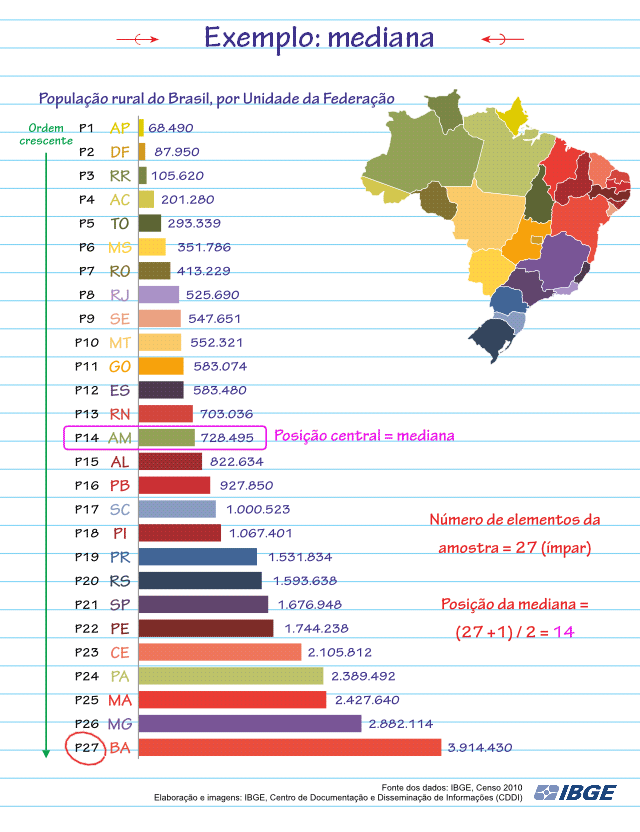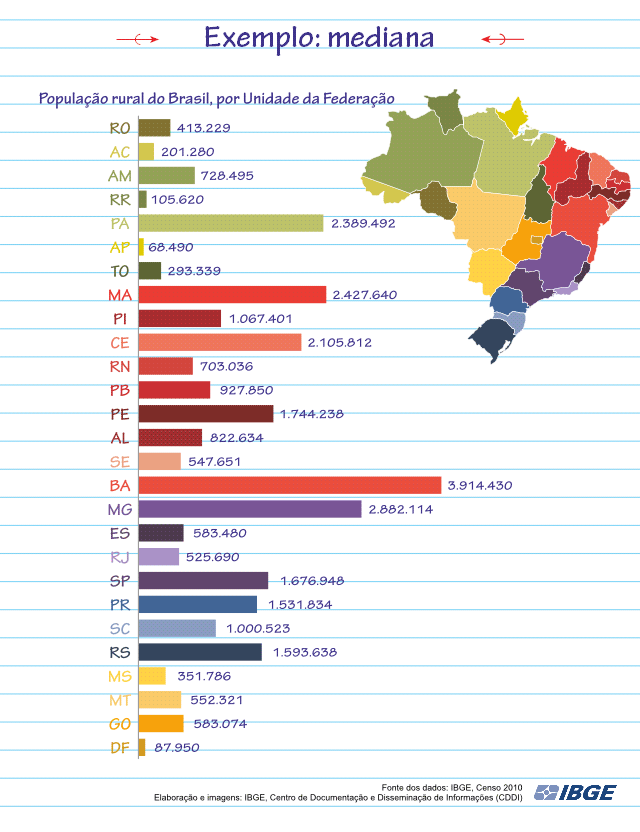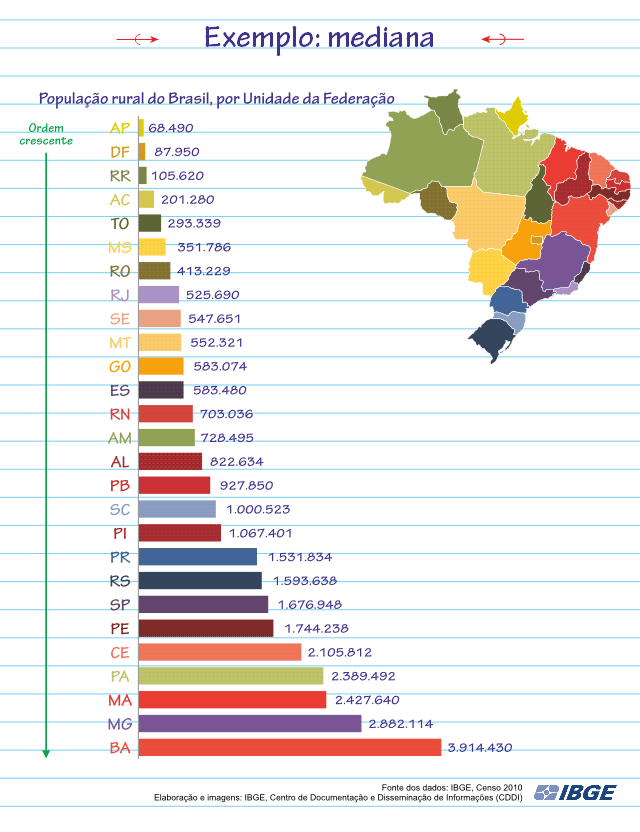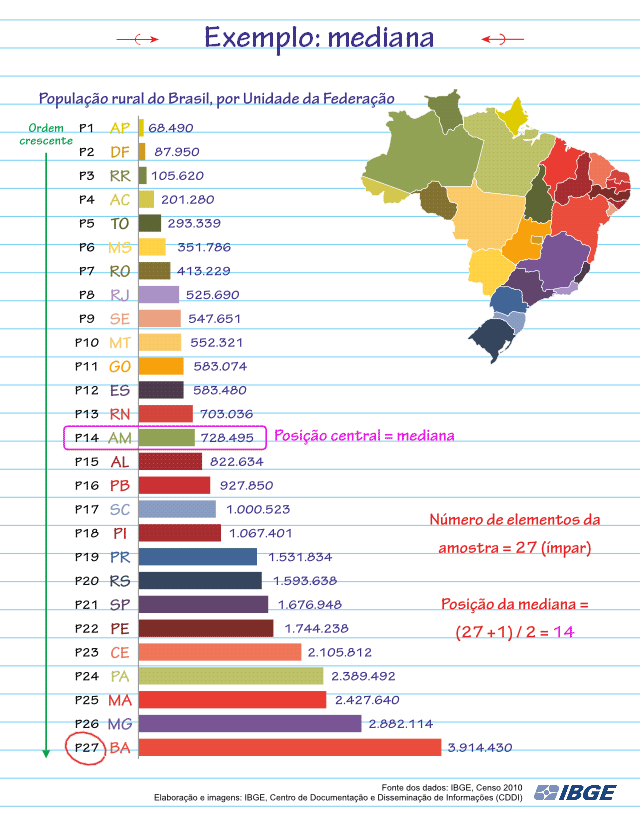
Como pode ser visto na animação, o valor da Mediana será 728.495.

Que informação nos fornece esta Mediana?

Ela nos diz que metade dos Estados do Brasil possui população rural menor ou igual a 728.495 e a outra metade possui população rural maior ou igual a 728.495.

Colocar o conjunto de dados (a nossa amostra) em uma ordem crescente para poder encontrar a Mediana nos revela outras duas informações também importantes: o Valor Mínimo e o Valor Máximo da amostra.

A Mediana se encontra exatamente entre o Valor Máximo − que é o último da amostra em ordem crescente − e o Valor Mínimo da amostra, que é o primeiro da amostra em ordem crescente.

No exemplo dos Estados da Federação, o Estado que possui a menor população rural (Valor Mínimo da amostra) é o Amapá, com 68.490 habitantes, e o Estado que possui a maior população rural (Valor Máximo da amostra) é a Bahia, com 3.914.430 habitantes.

Exemplo de cálculo da mediana com número par de elementos na amostra

Vamos, agora, utilizar um exemplo onde o número de elementos do conjunto de dados seja par.

Utilizemos o conjunto de dados formado pelo número de habitantes existentes nos municípios do Estado do Rio de Janeiro, conforme o Censo de 2010. A quantidade de municípios é de 92. A tabela com os dados dos municípios está disponível neste link.

Lembre-se que:
Se a quantidade de elementos da amostra for uma quantidade par, então a amostra terá dois elementos centrais e a Mediana será a Média Aritmética entre eles.

Devemos, então:

• Colocar os dados em ordem crescente;
• Encontrar o primeiro elemento da amostra para o cálculo da Mediana:
  Elemento da amostra que se encontra na posição 46: 34.410 (quantidade de residentes do município de Vassouras);
• Encontrar o segundo elemento da amostra para o cálculo da Mediana:
  Informação da amostra que se encontra na posição 47: 35.347 (quantidade de residentes do município de Casimiro de Abreu);
• A Mediana será a média aritmética entre esses dois valores:
  (34.410 + 35.347) / 2 = 34.878,5

Passamos a saber que:

• Valor Mínimo: 5.269 − O município de Macuco possui a menor quantidade de habitantes do Estado do Rio de Janeiro;
• Valor Máximo: 6.320.446 − O município do Rio de Janeiro possui a maior quantidade de habitantes do Estado do Rio de Janeiro;
• Como a Mediana é 34.878,5, então:
  • Metade (50%) dos municípios do RJ possui quantidade de habitantes menor que 34.878,5, e;
  • A outra metade (50%) possui a quantidade de habitantes maior que 34.878,5;
• O valor 34.878,5 não faz parte do conjunto de dados (amostra).

Saiba mais: Os Percentis

A Mediana também é chamada de Quartil − mais precisamente ela é chamada de Segundo Quartil.

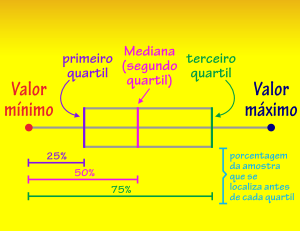Os Quartis dividem a nossa amostra em quatro partes iguais para melhor a observarmos:

• O Primeiro Quartil (Q1) é o valor que deixa 25% de nossa amostra abaixo e 75% de nossa amostra acima;
• O Terceiro Quartil (Q3) é o valor que deixa 75% de nossa amostra abaixo e 25% de nossa amostra acima;
• O Segundo Quartil (Q2) [a Mediana] é o valor que deixa 50% de nossa amostra abaixo e 50% de nossa amostra acima.

Referências

Estatística: entenda os conceitos de moda e mediana - Professores de Plantão